Surface Integral Of A Cylinder

Show Mobile Notice Bear witness All NotesHide All Notes

Mobile Observe

You appear to be on a device with a "narrow" screen width (i.e. you lot are probably on a mobile phone). Due to the nature of the mathematics on this site it is all-time views in landscape mode. If your device is not in mural style many of the equations will run off the side of your device (should be able to gyre to run into them) and some of the menu items will be cut off due to the narrow screen width.

Section half dozen-iii : Surface Integrals

It is at present time to call back about integrating functions over some surface, \(S\), in three-dimensional infinite. Permit's start off with a sketch of the surface \(South\) since the notation tin can get a little disruptive once we get into it. Here is a sketch of some surface \(Southward\).

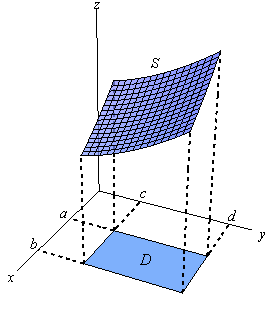
The region \(S\) will lie above (in this instance) some region \(D\) that lies in the \(xy\)-plane. We used a rectangle here, but it doesn't have to be of course. Besides annotation that we could simply as easily looked at a surface \(S\) that was in front of some region \(D\) in the yz­-plane or the \(xz\)-plane. Do not get so locked into the \(xy\)-plane that yous tin can't do bug that have regions in the other two planes.

At present, how nosotros evaluate the surface integral will depend upon how the surface is given to us. There are essentially two carve up methods here, although as we will see they are really the aforementioned.

First, let'southward wait at the surface integral in which the surface \(S\) is given by \(z = thou\left( {x,y} \right)\). In this example the surface integral is,

\[\iint\limits_{Due south}{{f\left( {x,y,z} \right)\,dS}} = \iint\limits_{D}{{f\left( {x,y,thou\left( {ten,y} \right)} \right)\sqrt {{{\left( {\frac{{\fractional thousand}}{{\partial 10}}} \correct)}^2} + {{\left( {\frac{{\partial g}}{{\partial y}}} \right)}^two} + i} \,dA}}\]

At present, we demand to be careful hither as both of these await similar standard double integrals. In fact the integral on the right is a standard double integral. The integral on the left however is a surface integral. The mode to tell them apart is by looking at the differentials. The surface integral will take a \(dS\) while the standard double integral volition have a \(dA\).

In order to evaluate a surface integral we volition substitute the equation of the surface in for \(z\) in the integrand and then add on the oft messy square root. After that the integral is a standard double integral and by this betoken nosotros should be able to bargain with that.

Note as well that there are similar formulas for surfaces given past \(y = g\left( {x,z} \right)\) (with \(D\) in the \(xz\)-plane) and \(ten = g\left( {y,z} \correct)\) (with \(D\) in the \(yz\)-plane). We will see ane of these formulas in the examples and we'll get out the other to you lot to write down.

The 2nd method for evaluating a surface integral is for those surfaces that are given by the parameterization,

\[\vec r\left( {u,v} \right) = 10\left( {u,v} \right)\vec i + y\left( {u,v} \right)\vec j + z\left( {u,5} \correct)\vec k\]

In these cases the surface integral is,

\[\iint\limits_{S}{{f\left( {x,y,z} \right)\,dS}} = \iint\limits_{D}{{f\left( {\vec r\left( {u,5} \right)} \right)\left\| {{{\vec r}_u} \times {{\vec r}_v}} \right\|\,dA}}\]

where \(D\) is the range of the parameters that trace out the surface \(S\).

Earlier we work some examples let'due south find that since we can parameterize a surface given by \(z = g\left( {x,y} \right)\) as,

\[\vec r\left( {ten,y} \right) = x\vec i + y\vec j + g\left( {x,y} \correct)\vec k\]

we tin can always use this course for these kinds of surfaces as well. In fact, it tin be shown that,

\[\left\| {{{\vec r}_x} \times {{\vec r}_y}} \right\|\, = \sqrt {{{\left( {\frac{{\partial g}}{{\fractional 10}}} \right)}^2} + {{\left( {\frac{{\partial g}}{{\partial y}}} \right)}^ii} + one} \]

for these kinds of surfaces. You lot might want to verify this for the exercise of calculating these cross products.

Let's work some examples.

Case 1 Evaluate \( \displaystyle \iint\limits_{S}{{6xy\,dS}}\) where \(S\) is the portion of the plane \(x + y + z = i\) that lies in the 1^st octant and is in front of the \(yz\)-airplane.

Show Solution

Okay, since we are looking for the portion of the plane that lies in forepart of the \(yz\)-plane nosotros are going to need to write the equation of the surface in the form \(x = g\left( {y,z} \right)\). This is easy enough to exercise.

\[x = one - y - z\]

Side by side, nosotros need to determine just what \(D\) is. Here is a sketch of the surface \(S\).

Here is a sketch of the region \(D\).

Discover that the axes are labeled differently than we are used to seeing in the sketch of \(D\). This was to keep the sketch consistent with the sketch of the surface. Nosotros arrived at the equation of the hypotenuse by setting \(x\) equal to nothing in the equation of the plane and solving for \(z\). Here are the ranges for \(y\) and \(z\).

\[0 \le y \le 1\hspace{0.25in}0 \le z \le 1 - y\]

At present, because the surface is non in the form \(z = g\left( {x,y} \right)\) we can't employ the formula to a higher place. However, as noted above we can modify this formula to get ane that will piece of work for us. Hither it is,

\[\iint\limits_{South}{{f\left( {x,y,z} \correct)\,dS}} = \iint\limits_{D}{{f\left( {g\left( {y,z} \right),y,z} \right)\sqrt {i + {{\left( {\frac{{\partial g}}{{\partial y}}} \right)}^2} + {{\left( {\frac{{\fractional g}}{{\partial z}}} \right)}^2}} \,dA}}\]

The changes fabricated to the formula should be the somewhat obvious changes. So, allow's do the integral.

\[\iint\limits_{South}{{6xy\,dS}} = \iint\limits_{D}{{6\left( {1 - y - z} \right)y\sqrt {1 + {{\left( { - one} \right)}^ii} + {{\left( { - 1} \right)}^ii}} \,dA}}\]

Notice that we plugged in the equation of the airplane for the x in the integrand. At this bespeak nosotros've got a fairly simple double integral to practice. Here is that work.

\[\begin{align*}\iint\limits_{S}{{6xy\,dS}} & = \sqrt 3 \iint\limits_{D}{{vi\left( {y - {y^2} - zy} \right)\,dA}}\\ & = half dozen\sqrt 3 \int_{{\,0}}^{{\,1}}{{\int_{{\,0}}^{{\,i - y}}{{y - {y^two} - zy\,dz}}\,dy}}\\ & = vi\sqrt 3 \int_{{\,0}}^{{\,1}}{{\left. {\left( {yz - z{y^2} - \frac{ane}{ii}{z^2}y} \right)} \correct|_0^{one - y}\,dy}}\\ & = 6\sqrt 3 \int_{{\,0}}^{{\,one}}{{\frac{1}{2}y - {y^two} + \frac{one}{2}{y^three}\,dy}}\\ & = 6\sqrt 3 \left. {\left( {\frac{one}{four}{y^two} - \frac{1}{iii}{y^iii} + \frac{ane}{8}{y^4}} \right)} \right|_0^one = \frac{{\sqrt 3 }}{4}\end{align*}\]

Example 2 Evaluate \( \displaystyle \iint\limits_{S}{{z\,dS}}\) where \(S\) is the upper one-half of a sphere of radius ii.

Evidence Solution

We gave the parameterization of a sphere in the previous department. Hither is the parameterization for this sphere.

\[\vec r\left( {\theta ,\varphi } \right) = ii\sin \varphi \cos \theta \,\vec i + 2\sin \varphi \sin \theta \,\vec j + 2\cos \varphi \,\vec g\]

Since nosotros are working on the upper half of the sphere here are the limits on the parameters.

\[0 \le \theta \le two\pi \hspace{0.5in}0 \le \varphi \le \frac{\pi }{2}\]

Next, we need to determine \({\vec r_\theta } \times {\vec r_\varphi }\). Hither are the two private vectors.

\[\begin{align*}{{\vec r}_\theta }\left( {\theta ,\varphi } \right) & = - 2\sin \varphi \sin \theta \,\vec i + 2\sin \varphi \cos \theta \,\vec j\\ {{\vec r}_\varphi }\left( {\theta ,\varphi } \right) & = 2\cos \varphi \cos \theta \,\vec i + 2\cos \varphi \sin \theta \,\vec j - 2\sin \varphi \,\vec k\end{align*}\]

Now let's take the cantankerous production.

\[\brainstorm{align*}{{\vec r}_\theta } \times {{\vec r}_\varphi } & = \left| {\begin{array}{*{20}{c}}{\vec i}&{\vec j}&{\vec m}\\{ - 2\sin \varphi \sin \theta }&{2\sin \varphi \cos \theta }&0\\{2\cos \varphi \cos \theta }&{2\cos \varphi \sin \theta }&{ - 2\sin \varphi }\end{assortment}} \correct|\\ & = - 4{\sin ^2}\varphi \cos \theta \,\vec i - 4\sin \varphi \cos \varphi {\sin ^2}\theta \,\vec thou - 4{\sin ^2}\varphi \sin \theta \,\vec j - 4\sin \varphi \cos \varphi {\cos ^2}\theta \,\vec k\\ & = - 4{\sin ^2}\varphi \cos \theta \,\vec i - 4{\sin ^ii}\varphi \sin \theta \,\vec j - 4\sin \varphi \cos \varphi \left( {{{\sin }^two}\theta \, + {{\cos }^2}\theta } \right)\vec k\\ & = - 4{\sin ^2}\varphi \cos \theta \,\vec i - 4{\sin ^ii}\varphi \sin \theta \,\vec j - 4\sin \varphi \cos \varphi \,\vec m\end{align*}\]

Finally, nosotros need the magnitude of this,

\[\begin{align*}\left\| {{{\vec r}_\theta } \times {{\vec r}_\varphi }} \right\| & = \sqrt {16{{\sin }^iv}\varphi {{\cos }^two}\theta + 16{{\sin }^4}\varphi {{\sin }^2}\theta + 16{{\sin }^2}\varphi {{\cos }^2}\varphi } \\ & = \sqrt {sixteen{{\sin }^4}\varphi \left( {{{\cos }^2}\theta + {{\sin }^2}\theta } \right) + 16{{\sin }^2}\varphi {{\cos }^ii}\varphi } \\ & = \sqrt {16{{\sin }^ii}\varphi \left( {{{\sin }^2}\varphi + {{\cos }^2}\varphi } \right)} \\ & = four\sqrt {{{\sin }^2}\varphi } \\ & = four\left| {\sin \varphi } \correct|\\ & = four\sin \varphi \finish{align*}\]

We can drop the absolute value bars in the sine because sine is positive in the range of \(\varphi \) that nosotros are working with. The surface integral is so,

\[\iint\limits_{S}{{z\,dS}} = \iint\limits_{D}{{2\cos \varphi \left( {iv\sin \varphi } \right)\,dA}}\]

Don't forget that we demand to plug in for \(x\), \(y\) and/or \(z\) in these equally well, although in this case we merely needed to plug in \(z\). Here is the evaluation for the double integral.

\[\begin{align*}\iint\limits_{S}{{z\,dS}} & = \int_{{\,0}}^{{\,2\pi }}{{\int_{{\,0}}^{{\,\frac{\pi }{2}}}{{4\sin \left( {2\varphi } \right)\,d\varphi }}\,d\theta }}\\ & = \int_{{\,0}}^{{\,ii\pi }}{{\left. {\left( { - 2\cos \left( {2\varphi } \right)} \right)} \right|_0^{\frac{\pi }{2}}\,d\theta }}\\ & = \int_{{\,0}}^{{\,2\pi }}{{4\,d\theta }}\\ & = viii\pi \end{marshal*}\]

Example 3 Evaluate \( \displaystyle \iint\limits_{South}{{y\,dS}}\) where \(South\) is the portion of the cylinder \({x^2} + {y^2} = 3\) that lies between \(z = 0\) and \(z = 6\).

Bear witness Solution

We parameterized up a cylinder in the previous department. Hither is the parameterization of this cylinder.

\[\vec r\left( {z,\theta } \right) = \sqrt 3 \cos \theta \,\vec i + \sqrt iii \sin \theta \,\vec j + z\,\vec thousand\]

The ranges of the parameters are,

\[0 \le z \le 6\hspace{0.25in}0 \le \theta \le 2\pi \]

At present we need \({\vec r_z} \times {\vec r_\theta }\). Here are the two vectors.

\[\begin{align*}{{\vec r}_z}\left( {z,\theta } \correct) & = \,\vec yard\\ {{\vec r}_\theta }\left( {z,\theta } \correct) & = - \sqrt 3 \sin \theta \,\vec i + \sqrt 3 \cos \theta \,\vec j\end{align*}\]

Hither is the cross product.

\[\begin{align*}{{\vec r}_z} \times {{\vec r}_\theta } & = \left| {\begin{assortment}{*{20}{c}}{\vec i}&{\vec j}&{\vec yard}\\0&0&1\\{ - \sqrt 3 \sin \theta }&{\sqrt 3 \cos \theta }&0\stop{assortment}} \right|\\ & = - \sqrt iii \cos \theta \,\vec i - \sqrt 3 \sin \theta \,\vec j\end{align*}\]

The magnitude of this vector is,

\[\left\| {{{\vec r}_z} \times {{\vec r}_\theta }} \right\| = \sqrt {3{{\cos }^2}\theta + three{{\sin }^2}\theta } = \sqrt 3 \]

The surface integral is and then,

\[\brainstorm{align*}\iint\limits_{S}{{y\,dS}} & = \iint\limits_{D}{{\sqrt 3 \sin \theta \left( {\sqrt 3 } \right)\,dA}}\\ & = 3\int_{{\,0}}^{{\,2\pi }}{{\int_{{\,0}}^{6}{{\sin \theta \,dz}}\,d\theta }}\\ & = 3\int_{{\,0}}^{{\,ii\pi }}{{6\sin \theta \,d\theta }}\\ & = \left. {\left( { - eighteen\cos \theta } \right)} \right|_0^{2\pi }\\ & = 0\end{align*}\]

Example 4 Evaluate \( \displaystyle \iint\limits_{South}{{y + z\,dS}}\) where \(S\) is the surface whose side is the cylinder \({x^2} + {y^ii} = iii\), whose bottom is the deejay \({x^2} + {y^2} \le 3\) in the \(xy\)-plane and whose peak is the plane \(z = 4 - y\).

Show Solution

There is a lot of information that we demand to go along rail of here. Showtime, we are using pretty much the same surface (the integrand is dissimilar however) as the previous example. Even so, different the previous example we are putting a top and bottom on the surface this time. Let'southward first start out with a sketch of the surface.

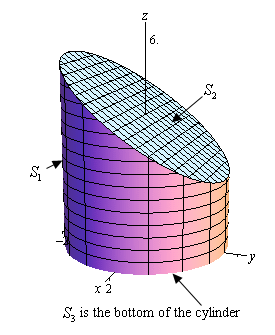
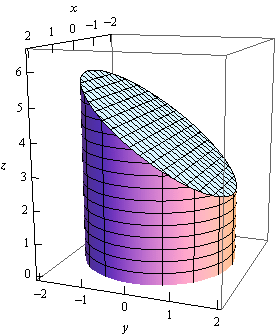
Nosotros need to be careful hither. At that place is more to this sketch than the bodily surface itself. We're going to let \({S_1}\) exist the portion of the cylinder that goes from the \(xy\)-plane to the aeroplane. In other words, the peak of the cylinder volition be at an angle. We'll call the portion of the aeroplane that lies inside (i.due east. the cap on the cylinder) \({S_2}\). Finally, the bottom of the cylinder (non shown here) is the disk of radius \(\sqrt iii \) in the \(xy\)-plane and is denoted by \({S_3}\).

In order to practice this integral we'll demand to note that just like the standard double integral, if the surface is split up upward into pieces we can likewise split the surface integral. So, for our case we volition have,

\[\iint\limits_{S}{{y + z\,dS}} = \iint\limits_{{{S_1}}}{{y + z\,dS}} + \iint\limits_{{{S_2}}}{{y + z\,dS}} + \iint\limits_{{{S_3}}}{{y + z\,dS}}\]

We're going to need to do three integrals here. However, we've done well-nigh of the work for the first i in the previous example and so permit's get-go with that.

\({S_1}\) : The Cylinder

The parameterization of the cylinder and \(\left\| {{{\vec r}_z} \times {{\vec r}_\theta }} \right\|\) is,

\[\vec r\left( {z,\theta } \correct) = \sqrt 3 \cos \theta \,\vec i + \sqrt 3 \sin \theta \,\vec j + z\,\vec k\hspace{0.5in}\left\| {{{\vec r}_z} \times {{\vec r}_\theta }} \right\| = \sqrt 3 \]

The departure between this problem and the previous one is the limits on the parameters. Here they are.

\[\begin{array}{c}0 \le \theta \le ii\pi \\ 0 \le z \le 4 - y = 4 - \sqrt three \sin \theta \end{assortment}\]

The upper limit for the \(z\)'south is the plane so nosotros can just plug that in. However, since we are on the cylinder we know what \(y\) is from the parameterization so nosotros will too demand to plug that in.

Here is the integral for the cylinder.

\[\begin{marshal*}\iint\limits_{{{S_1}}}{{y + z\,dS}} & = \iint\limits_{D}{{\left( {\sqrt three \sin \theta + z} \right)\left( {\sqrt 3 } \right)\,dA}}\\ & = \sqrt 3 \int_{{\,0}}^{{\,two\pi }}{{\int_{{\,0}}^{{4 - \sqrt three \sin \theta }}{{\sqrt iii \sin \theta + z\,dz}}\,d\theta }}\\ & = \sqrt 3 \int_{{\,0}}^{{\,2\pi }}{{\sqrt 3 \sin \theta \left( {4 - \sqrt 3 \sin \theta } \right) + \frac{1}{two}{{\left( {4 - \sqrt three \sin \theta } \right)}^2}\,d\theta }}\\ & = \sqrt 3 \int_{{\,0}}^{{\,2\pi }}{{8 - \frac{3}{ii}{{\sin }^2}\theta \,d\theta }}\\ & = \sqrt 3 \int_{{\,0}}^{{\,2\pi }}{{viii - \frac{iii}{iv}\left( {1 - \cos \left( {two\theta } \right)} \correct)d\theta }}\\ & = \sqrt 3 \left. {\left( {\frac{{29}}{iv}\theta + \frac{3}{viii}\sin \left( {two\theta } \right)} \right)} \right|_0^{2\pi }\\ & = \frac{{29\sqrt 3 \,\pi }}{2}\terminate{align*}\]

\({S_2}\) : Plane on Tiptop of the Cylinder

In this case nosotros don't need to practise any parameterization since information technology is gear up up to employ the formula that we gave at the start of this section. Remember that the plane is given past \(z = 4 - y\). As well note that, for this surface, \(D\) is the disk of radius \(\sqrt 3 \) centered at the origin.

Here is the integral for the plane.

\[\begin{marshal*}\iint\limits_{{{S_2}}}{{y + z\,dS}} & = \iint\limits_{D}{{\left( {y + 4 - y} \right)\sqrt {{{\left( 0 \right)}^2} + {{\left( { - 1} \correct)}^ii} + 1} \,dA}}\\ & = \sqrt 2 \iint\limits_{D}{{iv\,dA}}\stop{marshal*}\]

Don't forget that we need to plug in for \(z\)! At present at this indicate we can proceed in i of two ways. Either we tin keep with the integral or we tin call up that \(\iint\limits_{D}{{dA}}\) is nothing more than the area of \(D\) and we know that \(D\) is the disk of radius \(\sqrt 3 \) and so there is no reason to do the integral.

Hither is the residuum of the piece of work for this problem.

\[\begin{align*}\iint\limits_{{{S_2}}}{{y + z\,dS}} & = iv\sqrt two \iint\limits_{D}{{\,dA}}\\ & = 4\sqrt 2 \,\left( {\pi {{\left( {\sqrt 3 } \right)}^2}} \correct)\\ & = 12\sqrt 2 \,\pi \end{align*}\]

\({S_3}\) : Bottom of the Cylinder

Again, this is gear up up to apply the initial formula nosotros gave in this section once we realize that the equation for the bottom is given by \(g\left( {ten,y} \right) = 0\) and \(D\) is the disk of radius \(\sqrt 3 \) centered at the origin. Also, don't forget to plug in for \(z\).

Here is the work for this integral.

\[\brainstorm{align*}\iint\limits_{{{S_3}}}{{y + z\,dS}} & = \iint\limits_{D}{{\left( {y + 0} \correct)\sqrt {{{\left( 0 \right)}^2} + {{\left( 0 \right)}^two} + {{1}}} \,dA}}\\ & = \iint\limits_{D}{{y\,dA}}\\ & = \int_{0}^{{ii\pi }}{{\int_{0}^{{\sqrt 3 }}{{{r^2}\sin \theta \,dr}}\,d\theta }}\\ & = \int_{0}^{{2\pi }}{{\left. {\left( {\frac{1}{iii}{r^3}\sin \theta } \right)} \right|_0^{\sqrt 3 }\,d\theta }}\\ & = \int_{0}^{{ii\pi }}{{\sqrt iii \sin \theta \,d\theta }}\\ & = \left. { - \sqrt 3 \cos \theta } \right|_0^{2\pi }\\ & = 0\stop{align*}\]

We tin now get the value of the integral that we are subsequently.

\[\begin{align*}\iint\limits_{S}{{y + z\,dS}} & = \iint\limits_{{{S_1}}}{{y + z\,dS}} + \iint\limits_{{{S_2}}}{{y + z\,dS}} + \iint\limits_{{{S_3}}}{{y + z\,dS}}\\ & = \frac{{29\sqrt 3 \,\pi }}{2} + 12\sqrt 2 \,\pi + 0\\ & = \frac{\pi }{2}\left( {29\sqrt iii + 24\sqrt ii } \right)\stop{align*}\]

Surface Integral Of A Cylinder,

Source: https://tutorial.math.lamar.edu/classes/calciii/surfaceintegrals.aspx

Posted by: weaverdecroure.blogspot.com

Share this post